倒排索引求交算法相关资料调研
文章目录
1. IR-book 经典教材中的思路
Faster postings list intersection via skip pointers 通过跳指针,实现更快的 posting list 求交 https://nlp.stanford.edu/IR-book/html/htmledition/faster-postings-list-intersection-via-skip-pointers-1.html
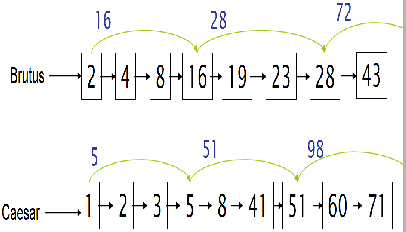
首先有个最 trival 的算法,两个 posting list,各一个指针,谁不匹配,就把谁右移一个,
跳表方法,思路类似 skip list,是要在建索引的时候,额外构建 skip list,这样就不是右移一个,而是按照跳表来右移。
2. lemire 教授的 SIMDCompressionAndIntersection 库中有多种算法
https://github.com/lemire/SIMDCompressionAndIntersection/blob/master/src/intersection.cpp
可以看到实现了这些求交算法,并且还有个 benchmark 程序 benchintersection 可以做对比
- “simd”
- “galloping”
- “scalar”
- “v1”
- “v3”
- “simdgalloping”
- “simd_avx2”
- “v1_avx2”
- “v3_avx2”
- “simdgalloping_avx2”
- “highlyscalable_intersect_SIMD”
- “lemire_highlyscalable_intersect_SIMD”
其中根据输入数据的规模,会选用不同的算法,并且还有 avx2 指令集的优化算法。
其中提到的 sse 优化的 fast-intersection-sorted-lists-sse https://highlyscalable.wordpress.com/2012/06/05/fast-intersection-sorted-lists-sse/
3. “The magic of Algorithms! " 中的算法
Chap. 6, Algorithm 6.1 Intersection based on Mutual Partitioning
http://didawiki.di.unipi.it/doku.php/magistraleinformaticanetworking/ae/ae2019/start#books_notes_etc
pdf 是 https://www.dropbox.com/s/dqttqigvuf4ydkd/main.pdf?dl=0
思路很简单,就是嵌套的 binary search,实测效果不错,而且实现简单,可以直接递归实现。
我实测效果还不错,提了个 issue https://github.com/lemire/SIMDCompressionAndIntersection/pull/29
4. List Intersection for Web Search: Algorithms, Cost Models, and Optimizations
http://www.vldb.org/pvldb/vol12/p1-kim.pdf 微软的文章,搞了个 cost model, 来评估各种 list 求交集算法的性能,但是不开源。
本文提出一种基于代价的模型,来估算各种算法组合的代价,并使用代价模型来搜索代价最低的算法,得到的计划通常是 2-way 算法的一个组合, 并且比传统的 2-way 和 k-way 算法性能都好。
并列举了常见的 List Intersection 算法: 2-way:
- 2-Gallop
- 2-Merge
- 2-SIMD
k-way:
- k-Gallop
- k-Merge
2-way vs. k-way 本文断言,对 k-list 求交,通过 k-1 次重复 2-way 求交算法,比通过单次 k-way 求交算法,更快。
结论,通过本文 cost model optimizer 规划出来的 2-way 求交计算,通常比 k-way 求交更快。
https://arxiv.org/pdf/1401.6399.pdf
We demonstrated that combining unpacking and differential coding resulted in faster decompression speeds, which were approximately 30 % better than the best speeds reported previously [3]. To match the performance of these fast compression schemes, we additionally vectorized and optimized the intersection of posting lists. To this end, we introduced a family of algorithms exploiting commonly available SIMD instructions (V1, V3 and SIMD GALLOPING). They are often twice as fast as the best non-SIMD algorithms. Then, we used our fast SIMD routines for decompression and posting
Efficient set intersection for inverted indexing
http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.415.2636&rep=rep1&type=pdf
Intersection in integer inverted indices https://pdfs.semanticscholar.org/db30/9935b512ef4d0c8941c96e987ad70400ebde.pdf
lookup 算法最快,非常简单,两层存储,按位分成两层。 首层直接定位,二层直接遍历。 二层可以压缩。